Murrey Math
T. Henning Murrey
T. Henning Murrey from Nashville Tennessee was born in 1942. In 1993 Murrey worked on theories of random
thinking, importantly by NOT studying the market. From this he wrote his trading book and then in 1995 Murrey?
rediscovered? what Gann hinted at in his book, the six clues. Murrey translated the algorithms of a Fractal
inside a Cube set to the Base Ten to exact Fibonacci Ratios set to the scale of Music.
The main assumption in Murrey Math is that all markets behave in the same manner akin to a herd.
This agrees with our concept of reflexability, that the market in a constant state of flux or perpetual chaos.
As such the market is seeking to find equilibrium, which is the point of extreme chaos, (i.e. Tops and bottoms
or inflexion points). These are also the points of extreme market behavior, and why we place so much value on
sentiment indicators. What we found was that The Murrey Math trading system is primarily based upon the
observations made by W.D. Gann in the first half of the 20?th century. While Gann was purported to be a
brilliant trader in any market his techniques have been regarded as complex and difficult to implement.
The great contribution of Murrey Math (T. H. Murrey) was the creation of a system of geometry that can be used
to describe market price movements in time. This geometry facilitates the use of Gann’s trading techniques.
Significantly it added the turning point methodology that eluded us in refining Fibonacci levels. The Murrey
Math Trading system works totally in harmony with our Gann Fans and Angles.
MM Line Interpretation
Murrey Math is a trading system for all equities. This includes stocks, bonds, futures (index, commodities,
and currencies), and options. The main assumption in Murrey Math is that all markets behave in the same manner
(i.e. all markets are traded by a mob and hence have similar characteristics.). The Murrey Math trading system
is primarily based upon the observations made by W.D. Gann in the first half of the 20th century. While Gann was
purported to be a brilliant trader in any market his techniques have been regarded as complex and difficult to
implement. The great contribution of Murrey Math (T. H. Murrey) was the creation of a system of geometry that
can be used to describe market price movements in time. This geometry facilitates the use of Gann's trading
techniques.
The Murrey Math trading system is composed of two main components; the geometry used to gauge the price
movements of a given market and a set of rules that are based upon Gann and Japanese candlestick formations.
The Murrey Math system is not a crystal ball, but when implemented properly, it can have predictive capabilities.
Because the Murrey Math rules are tied to the Murrey Math geometry, a trader can expect certain pre-defined
behaviors in price movement. By recognizing these behaviors, a trader has greatly improved odds of being on the
correct side of a trade. The overriding principle of the Murrey Math trading system is to recognize the trend of
a market, trade with the trend, and exit the trade quickly with a profit (since trends are fleeting). In short,
"No one ever went broke taking a profit".
The Murrey Math geometry mentioned above is "elegant in its simplicity". Murrey describes it by saying,
"This is a perfect mathematical fractal trading system". An understanding of the concept of a fractal is
important in understanding the foundation of Murrey Math. For readers interested in knowing more about fractals
I would recommend the first 100 pages of the book,"The Science of Fractal Images" edited by Heinz-Otto Peitgen
and Dietmar Saupe. The book was published by Springer-Verlag, copyright 1988. An in depth understanding of
fractals requires more than "8'th grade math", but an in depth understanding is not necessary (just looking at
the diagrams can be useful).
The size (scale) of basic geometric shapes are characterized by one or two parameters. The scale of a circle
is specified by its diameter, the scale of a square is given by the length of one of its sides, and the scale of
a triangle is specified by the length of its three sides. In contrast, a fractal is a self similar shape that is
independent of scale or scaling. Fractals are often constructed by repeating a process recursively over and over.
The next question, of course is, "What does a fractal have to do with trading in equity markets?" Imagine if
someone presented you with a collection of price-time charts of many different equities and indices from many
different markets. Each of these charts has been drawn using different time scales. Some are intraday, some are
daily, and some are weekly. None of these charts, however, is labeled. Without labels, could you or anyone else
distinguish a daily chart of the Dow from a weekly chart of IBM, or from an intraday chart of wheat prices.
Not very likely. All of these charts, while not identical, appear to have the same general appearance.
Within a given time period the price moves some amount, then reverses direction and retraces some of its prior
movement. So, no matter what price-time scales we use for our charts they all look pretty much the same
(just like a fractal). The "sameness" of these various charts can be formally characterized mathematically
(but this requires more that 8th grade math and is left as an exercise to the interested reader).
Gann was a proponent of "the squaring of price and time", and the use of trend lines and various geometric
angles to study price-time behavior. Gann also divided price action into eighths. Gann then assigned certain
importance to markets moving along trend lines of some given angle. Gann also assigned importance to price
retracements that were some multiple of one eighth of some prior price movement. For example, Gann referred to
movement along the 45 degree line on a price-time chart as being significant. He also assigned great significance
to 50% retracements in the price of a commodity. The question is, "A 45 degree angle measured relative to what?"
"A 50% retracement relative to what prior price?"
These angle or retracement measurements are made relative to Gann's square of price and time. Gann's square
acted as a coordinate system or reference frame from which price movement could be measured. The problem is that
as the price of a commodity changes in time, so must the reference frame we are using to gauge it. How should the
square of price and time (the reference frame) be changed so that angles and retracements are measured
consistently?
This question is one of the key frustrations in trying to implement Gann's methods. One could argue that Gann
recognized the fractal nature of market prices changing in time. Gann's squaring of price and time, however,
did not provide an objective way of quantifying these market price movements. If one could construct a consistent
reference frame that allowed price movement to be measured objectively at all price-time scales, then one could
implement Gann's methods more effectively. This is exactly what Murrey Math has accomplished.
Here below is a short description extracted from a document published a few years ago by Tim Kruzel ,
which since seems to have disappeared from the face of the WWW.
What each MML represents?
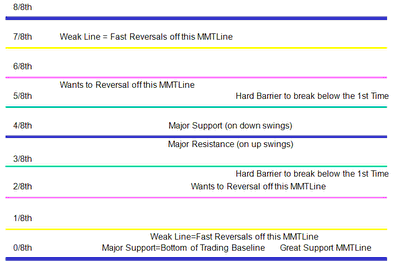
 This graphic illustrates the following:
This graphic illustrates the following:
8/8: Hardest line to rise above (overbought)
7/8: Fast reverse line (weak)
6/8: Pivot reverse line
5/8: Upper trading range
----------------------------------------
----------------------------------------
3/8: Lower trading range
2/8: Pivot reverse line
1/8: Fast reverse line (weak)
0/8: Hardest line to fall below (oversold)
Price is between 3/8 and 5/8 MML's about 43% of the time.
Here is another graphic illustrating the buy/sell options:
As you start observing the interaction between price and MML's, you'll start to notice some patterns.
Take a look at these:
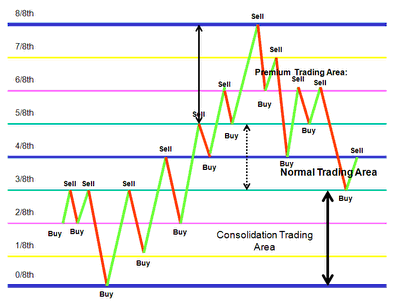
What this is showing us is that many times, if price is above the 5/8 line and falling, it will generally
stop and consolidate around 5/8 first before heading lower. The same is true in the opposite direction:
if price is below the 3/8 line and rising, it will generally stop and consolidate around the 3/8 line before
heading higher.
On top of that, if price is between the 5/8 line and 6/8 line and heading higher, the tendency is to bounce
off/reverse off the 6/8 line and retest 5/8 before heading higher. The same is true for shorts, if price is
between the 3/8 line and 2/8 line and heading lower, it tends to bounce off the 2/8 line and retest 3/8 before
heading lower.
Why does price do this? Remember, price is between the 3/8 and 5/8 line about 43% of the time. So before it
jumps outside of its comfort zone, it needs to be sure (hence the retest).
Now let's take a quick look at what happens when price moves above 8/8 or below 0/8. This does not occur too
often, but when it does it's important to know what to expect.
The above illustration tells us the following: If price moves above 8/8, 75% of the time the price will reverse
off the +1/8 line and retest 8/8 before moving higher to +2/8. Similarly, if price falls below 0/8, 75% of the
time the price will reverse off the -1/8 line and retest 0/8 before moving lower to -2/8.
Now, if price moves beyond the +1/8 or -1/8 lines, then 95% of the time it will reverse when it hits +2/8 or
-2/8. Remember, the market was already in overbought (8/8) or oversold (0/8) mode, so once we push that to the
extreme (+2/8 or -2/8) it is extremely unlikely (95% chance) to reverse.
Check out this illustration to see it demonstrated: